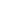C/C++ 哈夫曼树的构造、编码以及译码

《题目》：假设用于通信的电文由字符集{a,b,c,d,e,f,g,h}中的字母构成，这8个字母在电文中出现的 频率分别为：{0.19, 0.21, 0.02, 0.03, 0.06, 0.07, 0.1, 0.32}.
要求：画出哈夫曼树。

---

我从课本上面摘抄了一个题目，题目大概是上面这样的，我们这里只是详细的说明一下哈弗曼树要怎么构建。借用一下这个题目。

哈夫曼树的构造

分析：我们这里直接将小数整数化，容易看出大小来。

①8个结点的权值大小如下：

②从19，21，2，3，6，7，10，32中选择两个权小结点。选中2，3。同时算出这两个结点的和5。

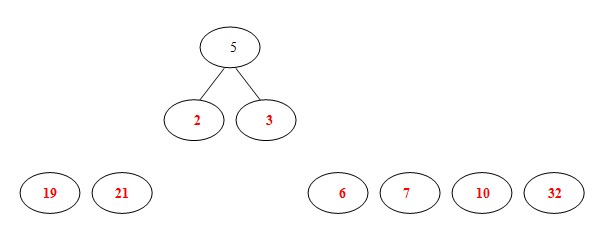
③从19，21，6，7，10，32，5中选出两个权小结点。选中5，6。同时计算出它们的和11。

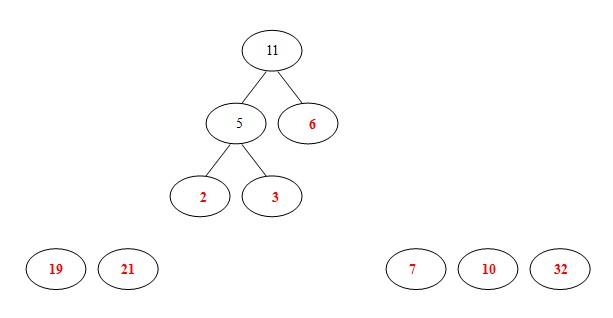
④从19，21，7，10，32，11中选出两个权小结点。选中7，10。同时计算出它们的和17。
注：这时选出的两个数字都不是原来的二叉树里面的结点，所以要另外开一棵二叉树。

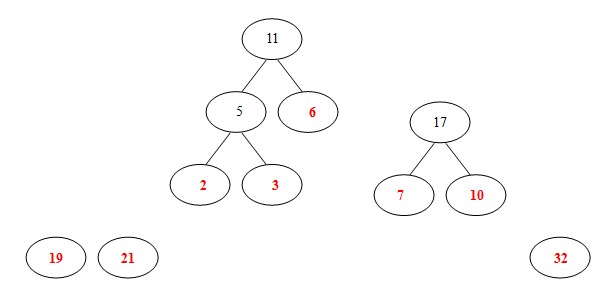
⑤从19，21，32，11，17中选出两个权小结点。选中11，17。同时计算出它们的和28。

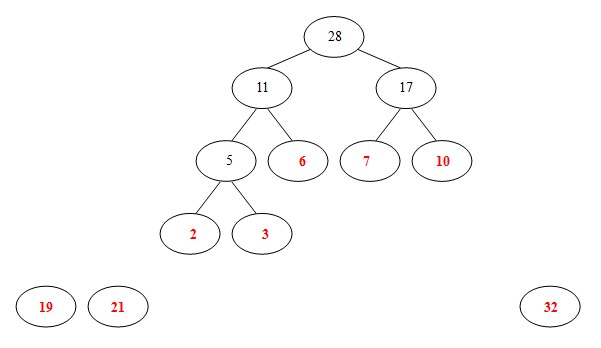
⑥从19，21，32，28中选出两个权小结点。选中19，21。同时计算出它们的和40。 另起一颗二叉树。

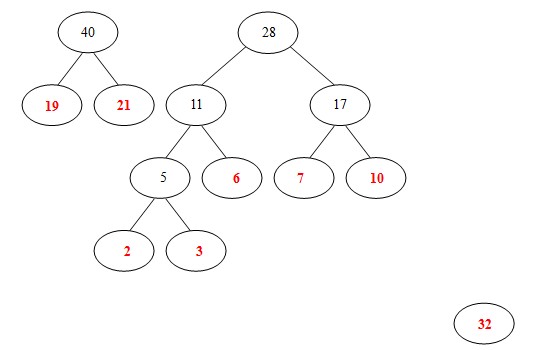
⑦从32，28， 40中选出两个权小结点。选中28，32。同时计算出它们的和60。

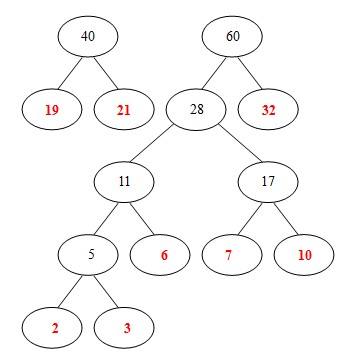
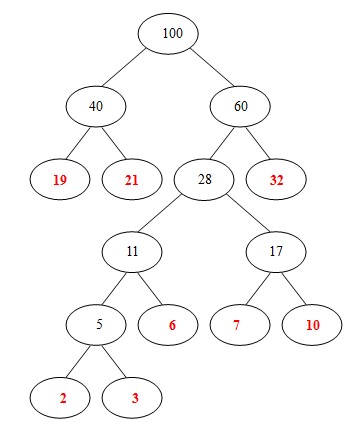
⑧从 40， 60中选出两个权小结点。选中40，60。同时计算出它们的和100。 好了，此时哈夫曼树已经构建好了。

ps:上次做作业的时候，我构造哈弗曼树就是一直从剩下的结点里面找权值最小的，然后添加上去，而没有考虑构造出来的”和”权值的大小问题。导致哈夫曼树构造错误！

哈夫曼编码及译码的实现

#include<stdio.h>
#include<string.h>
#include<stdlib.h>

//树结点定义
typedef  struct 
{
    int weight;
    int parent;
    int lchild;
    int rchild;
}HTNode,*HuffmanTree;

static char N[100];//用于保存正文

//哈弗曼编码，char型二级指针
typedef char **HuffmanCode;

//封装最小权结点和次小权结点
typedef  struct 
{
    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
AI写代码